掌握这些套路，轻松解决递归算法问题

jerry.mei

2020年08月21日 • 17 min read

算法问题，我们通常解决的途径无非就是迭代和递归。大部分人可能倾向于使用迭代的思想来解决算法问题，因为一方面我们清楚每一步计算机是怎么去执行的，另一方面我们常常被灌输递归效率很低的思想。

但递归本身也是应用非常广泛的算法，像深度优先搜索、前中后序二叉树遍历等问题都可以用递归来轻松解决的。而且，像函数式编程语言，由于它不像命令式编程那样去关心解决问题的步骤，所以更倾向于用递归而不是迭代。

image_1egislr4h1kpk7021jnmvum1an49.png-23.8kB

递归为什么那么难

对于递归的理解，其实就是一个先递进，再回归的过程。知乎上有一篇答案写的很不错，这里就不多做介绍了：对于递归有没有什么好的理解方法？

像阶乘问题，斐波那契数列问题，我们看完都会觉得递归很简单，因为我们完全可以通过公式推导出来。但在实际的应用中，更复杂一点的情况，就不知道怎么去用了。即使去读别人写好的递归代码，也不一定读的懂。这是大部分人普遍的体会。

在王争的《数据结构与算法之美》专栏中，他就提到过从他自己学习数据结构和算法的经历来看，有两个最难理解的知识点，一个是动态规划，另一个就是递归。

所以这里要告诉大家的是，读不懂递归代码跟我们的水平没有多大关系，不论是算法菜鸟还是刷题高手。因为我们通常所谓的读懂代码，就是在大脑里模拟计算机执行到某一步得到的结果是什么。对于迭代算法来说，这没什么问题。对于递归算法的话，这样去理解的话，就进入了一个思维误区。不信，大家去打断点调试一下递归代码执行的过程，大概率是懵逼的😭

我们大脑几乎没办法把整个递和归的过程一步步都想清楚，所以不要尝试用人脑去分解递归的每个步骤。简单来说，就是忘掉递归的过程。

递归这门功夫是需要我们废掉先前学会的武功的

递归三要素

不去理解递归的过程，那么我们用什么方式去解决递归问题呢？我们拿阶乘问题来举例说明：

6! = 6*5!
5! = 5*4!
...
2! = 2

对于6!的问题，我们可以拆解为 6*5!的问题，一直拆解到2!等于它自己。所以我们可以总结出一些规律：

一个问题的解可以分解为几个子问题的解
这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
存在递归终止条件

对于大问题拆解为若干子问题的思路，其实用到了分治算法（divide and conquer， D&C）的思想。分治算法的步骤就是：

找出基线条件，这种条件必须尽可能简单
不断将问题分解（或者说缩小规模），直到符合基线条件

综上，我们可以总结出递归的三要素

第一要素：明确函数想要干什么

对于递归，很重要的一件事就是，这个函数的功能是什么，它要完成什么样的一件事。而这个，是完全由我们自己来定义的。我们先不管函数里面的代码是什么，而是要先明白，这个函数是要用来干什么。

ps：这一点，大家可能觉得是废话。先不要妄下结论，递归三要素缺一不可，同等重要。

第二要素：寻找基线条件

找出基线条件（base case）。基线条件指的是函数不再调用自己，从而避免形成无限循环的条件。

第三要素：寻找递归条件

找出递归条件（recursive case），也就是函数的等价关系式。利用分治的思想，把大问题拆解为小问题，不断缩小参数的范围。

递归套路

下面是写递归代码非常重要的思想，我们姑且称为递归套路吧。

递归三要素
写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。（代码是基于三要素翻译出来的，不是直接写出来的）
需要注意的是，我们平时写代码都会试图搞清楚计算机每一步都是怎么执行的。对于递归代码，这种试图想清楚整个递和归过程的做法，实际上是进入了一个思维误区。
如果一个问题 A 可以分解为若干子问题 B、C、D，我们可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A。

案例分析

接下来，我会举一些难度越来越大的案例来带大家实践一下递归的套路是如何运用的。

`入门级`

1. 阶乘问题

示例：求6的阶乘

我们先忘记阶乘的公式推导，用递归三要素来解决：

第一步，明确函数干什么：计算阶乘

function factorial(n){}

6 的阶乘就是 factorial(6)

第二步，找出基线条件

1 的阶乘为 1
2 的阶乘为 2

factorial(1) == 1
factorial(2) == 2

function factorial(n){
  if(n == 1){
    return 1
  }
  if(n == 2){
    return 2
  }
}

重构一下代码：

function factorial(n){
  if(n<=2){
    return n
  }
}

第三步：利用分治的思想，缩小问题的规模。也就是寻找等价关系

factorial(6) = 6*5*4*3*2*1
factorial(5) = 5*4*3*2*1

等价关系

factorial(6) = 6 * factorial(5)
factorial(n) = n * factorial(n-1)

最终翻译出计算阶乘的递归代码：

function factorial(n){
  if(n<=2){
    return n
  }
  return n * factorial(n-1)
}

2. 斐波那契数列

示例：1、1、2、3、5、8、13、21、34.... 前两项之和等于后一项。求第n项的值

跟第一题的解法一样。

第一步：明确函数干什么

function fibonacci(n){}

第二步：找出基线条件

fibonacci(1) == 1
fibonacci(2) == 1

function fibonacci(n){
  if(n<=2){
    return 1
  }
}

第三步：找出递归条件

fibonacci(7) == fibonacci(5) + fibonacci(6)
fibonacci(n) == fibonacci(n-2) + fibonacci(n-1)

最终代码如下：

function fibonacci(n){
  if(n<=2){
    return 1
  }
  return fibonacci(n-2) + fibonacci(n-1) 
}

3. 分地问题（欧几里得算法）

示例：长宽分别为 1680m，640m的地，均匀分成方块，且分出的方块尽可能大。

该问题等同于求最大公约数问题，使用欧几里得算法。

1680 % 640 = 400     2块 640x640的地，1块 640x400的地
640 % 400 = 240
400 % 240 =  160
240 % 160 = 80
160 % 80 = 0

最终得到的最大方块是 80 平方

第一步：明确函数干什么

function gcd(a,b){}

第二步：找出基线条件

160 x 80 ，一条边是另一条边的整数倍

function gcd(a,b){
  if(a%b == 0){
    return b
  }
}

第三步：找出递归条件

gcd(1680, 640) == gcd(640, 400)
gcd(a, b) == gcd(b, a % b)

function gcd(a,b){
  if(a%b == 0){
    return b
  }
  return gcd(b, a % b)
}

总结：递归问题基本逃不开阶乘问题，斐波那契数列问题。但上面三个例子对于解决递归这一类型的问题并没有提供很好的思路，因为过于简单。通过纯数学推导我们就可以得出公式，用不用递归的套路都无所谓。

`中级`

4. 反转链表

https://leetcode-cn.com/problems/reverse-linked-list/

反转链表问题是一个很有代表性的问题，leetcode 官方题解里的递归写法，很多人表示看不懂。看不懂就对了！我们用递归的套路来解决。

第一步：定义一个反转单链表的函数，参数为链表的第一个节点

function reverseList(head){}

第二步：找出基线条件，当链表为空或者链表只有一个节点，返回链表本身即可

function reverseList(head){
  if(head == null || head.next == null){
    return head
  }
}

第三步：问题拆解

前面的几个例子，等价关系通过公式推导就很容易得出。这个例子就没有那么直观了。同样，我们用分治的思想，把大问题拆小

reverseList (1->2->3->4) 拆成 1 和 reverseList(2->3->4)的问题。代码如下：

function reverseList(head){
  if(head == null || head.next == null){
    return head
  }
  const newList = reverseList(head.next)
}

前面总结的有两句话在这里就变得极为重要了：

递归三要素的第一点：明确你这个函数想要干什么
如果一个问题 A 可以分解为若干子问题 B、C、D，你可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A

我们可以画一下链表的结构，最开始如下：

那么，我们可以理解为我们写了一个叫reverseList(node)的函数，它的作用就是反转链表。并且我们假设reverseList(2->3->4)的问题已经解决了，也就是说2->3->4已经反转为4->3->2了。我们先把已经反转的链表保存起来。

现在链表如下：

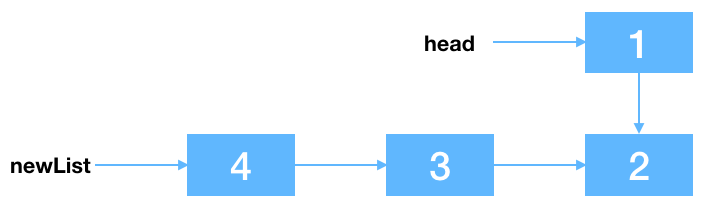
1 的 next 还是 2，newList现在为 4->3->2

我们在这个基础上解决 1 的问题，只需要把节点 2 的 next 指向 1，然后把 1 的 next 指向 null，就可以了。最后返回这个新的链表。

function reverseList(head){
  if(head == null || head.next == null){
    return head
  }
  const newList = reverseList(head.next)
  head.next.next = head
  head.next = null
  return newList
}

总结：这道题很具有代表性，因为我们递归的套路里面列举的都用上了。如果我们直接看最后写出来的代码，去思考计算机是怎么执行的，估计想很久都想不明白。所以对于递归问题，千万不要去想计算机是怎么去执行的。

5. 数组转多叉树

示例：把下面的数组转换成树状结构

- 全部文件
  - 图片
    - 壁纸
      - 风景
      - 动漫
      - 游戏
    - 头像
  - 文档
  - 视频
    - 电影
    - 纪录片

[
      { id: 1, name: '全部文件', parent_id: null },
      { id: 2, name: '图片', parent_id: 1 },
      { id: 3, name: '文档', parent_id: 1 },
      { id: 4, name: '视频', parent_id: 1 },
      { id: 5, name: '壁纸', parent_id: 2 },
      { id: 6, name: '头像', parent_id: 2 },
      { id: 7, name: '电影', parent_id: 4 },
      { id: 8, name: '纪录片', parent_id: 4 },
      { id: 9, name: '风景', parent_id: 5 },
      { id: 10, name: '动漫', parent_id: 5 },
      { id: 11, name: '游戏', parent_id: 5 }
]

第一步：明确函数干什么

function arr2Tree(arr){}

第二步：找出基线条件，如果 arr 为空数组，直接返回空数组

function arr2Tree(arr){
  if(arr.length == 0){
    return arr
  }
}

第三步：大问题拆解，把数组的第一项拿出来，数组剩余的部分继续做 arr2Tree 操作

假设剩下的部分已经转换成 tree 了，代码如下

function arr2Tree(arr){
  if(arr.length == 0){
    return arr
  }
  const head = arr[0]
  const rest = arr.slice(1)
  const tree = arr2Tree(rest)
}

然后我们只需解决数组第一项的问题，把它跟余下的已经转换为 tree 的数据合并为一个 tree

{ id: 1, name: '全部文件', parent_id: null }

[
    { id: 2, name: '图片', childern:[...] },
    { id: 3, name: '文档' },
    { id: 4, name: '视频', children: [...] }
]

对于第一项的问题，我们只需要遍历余下的数组，判断 parent_id 是否是等于第一项的 id，如果是就是它的子节点；如果不是，就跟它是兄弟节点

function arr2Tree(arr) {
  if (arr.length == 0) {
    return arr
  }
  const head = arr[0]
  const tree = arr2Tree(arr.slice(1))
  const childrens = [], siblings = [];
  for (let i = 0; i < tree.length; i++) {
    if (head.id == tree[i].parent_id) {
      childrens.push(tree[i])
    } else {
      siblings.push(tree[i])
    }
  }
  if (childrens.length > 0) {
    head.children = childrens
  }
  return [head].concat(siblings)
}

另一种写法：找儿子

上面这种写法是把整个数组拆分成[head | rest]，然后去解决问题的。对于问题的拆解，我们通常可能会有不同的思路，所以递归的写法也是不尽相同的。

比如，数组转树的问题，我们可以遍历这个数组，先找 null 的儿子，可能找不到，也可能找到多个。这里，我们找到的是1。然后再去找1的儿子，也是一样的，我们找到了2、3、4，依此类推。

第一步：明确函数干什么

跟前面不一样的是，我们这里传入了两个参数，一个是数组arr，另一个是我们要找谁的儿子pid

function arr2Tree(arr, pid){}

第二步：找出基线条件

在整个数组中找儿子，可能找不到。这个例子基线条件其实没有那么明显，遍历整个数组，遍历完了都没找到儿子。那么什么都不做就行了。

function arr2Tree(arr, pid) {
  arr.forEach(item => {
    if (item.parent_id === pid) {
			...
    }  
  });
}

第三步：大问题拆解

我们把问题分解为找 null 的儿子 1，以及 1 的儿子 2、3、4...

我们假设找 1 的儿子的问题已经解决，再来看找 null 的儿子的问题。

找到的结果可能有多个，我们保存在res里，最终返回这个res即可。

function arr2Tree(arr, pid) {
  const res = [];
  arr.forEach(item => {
    if (item.parent_id === pid) {
       res.push(item)
    }  
  });
  return res
}

也有可能没找到儿子。那么对于前面我们假设找 1 的儿子的问题已经解决了这种情况。它也是要么找到了儿子，返回res；要么没找到，返回[]。

所以我们可以根据返回的结果来做个判断。如果当前选项的儿子找到了儿子，我们给它追加一个children属性就可以了，用来存放它的儿子。

function arr2Tree(arr, pid) {
  const res = [];
  arr.forEach(item => {
    if (item.parent_id === pid) {
      const result = arr2Tree2(arr, item.id);
      if (result.length) {
        item.children = result;
      }
      res.push(item)
    }  
  });
  return res
}

6. 多叉树的前序遍历（深度优先遍历）

二叉树是先遍历根，再遍历左子树，再遍历右子树。对于多叉树，原理相同，区别就是遍历左子树和右子树变成循环对子树进行递归遍历算法。

对于下面的多叉树，前序遍历输出的结果是：

A->B->B1->B11->B12->B13->B2->C->C1->C2->D->D1

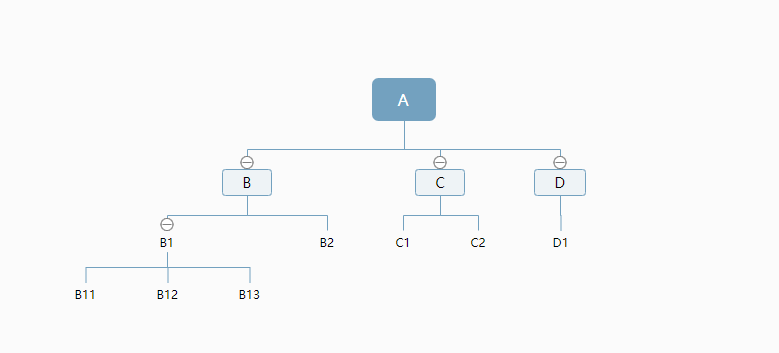
image_1egj4q1vv1ld11lfi16pf1god1jlkm.png-10.2kB

第一步：明确函数干什么

function preOrderTraverse(root) {}

第二步：找出基线条件

对于多叉树，我们对它进行前序遍历，当遍历到叶子节点的时候，就结束了。所以结束条件就是判断一个节点是否是叶子节点。

function preOrderTraverse(root) {
  if (root.childeren == null) {
    return
  }
}

第三步：大问题拆解

对于多叉树而言。我们有一个根节点，然后根节点下有几个孩子。我们假设它的孩子的问题已经解决了。那么我们解决这个根节点的问题就行了。

所以，我们首先访问根节点本身，再依次访问它的孩子。

function preOrderTraverse(root) {
  console.log(root)
  if (root.childeren == null) {
    return
  }
  for (let item of root.childeren) {
    preOrderTraverse(item)
  }
}

7. 多叉树的层序遍历（广度优先遍历）

层序遍历，一层一层的访问树的节点。通常可以用这种方式来求树的深度。在处理现实问题，比如部门树，我们要限制子部门的深度，就可以用层序遍历来实现。

对于上面的多叉树，层序遍历输出的结果是

A->B->C->D->B1->B2->C1->C2->D1->B11->B12->B13

树的层序遍历用递归可能不太好理解，因为树的根节点只有一个，但它的孩子节点有多个。这样去推导的时候，数据类型不一致。

我们转化成森林的层序遍历就好理解了。

森林是由若干棵树组成的。层序遍历可以先访问森林的第一层，再访问森林的第二层，依次类推。

我们可以确定递归的参数为每一层的节点组成的数组，森林的第一层为[root]

第一步：明确函数干什么

//nodes 为森林每一层节点组成的数组
function levelOrderTraverse(nodes) {}

第二步：找出基线条件

基线条件也很好确定了，如果传入的nodes为空，就结束掉

function levelOrderTraverse(nodes) {
  if(nodes.length == 0){
    return
  }
}

第三步：大问题拆解

分解问题，假设第二层的节点的问题已经解决。我们来处理第一层节点的问题。

那么我们只需要遍历第一层的所有节点，打印它们即可。

function levelOrderTraverse(nodes) {
  if (nodes.length == 0) {
    return;
  }
  for (let item of nodes) {
    console.log(item.name)
  }
}

前面我们说假设第二层的节点的问题已经解决，也就是levelOrderTraverse([第二层节点的集合])。那么我们在第一层只需要得到第二层的节点的集合就可以了。

我们使用一个 temp 数组来存放第二层节点的值，也就是说如果第一层节点遍历的时候，它有 children 就保存到 temp 数组中。

function levelOrderTraverse(nodes) {
  if (nodes.length == 0) {
    return;
  }
  let temp = []
  for (let item of nodes) {
    console.log(item.name)
    if (item.childeren != null) {
      temp = temp.concat(item.childeren)
    }
  }
  levelOrderTraverse(temp)
}

练习

在排序算法中，像快排和归并排序用递归也可以很好地解决，有兴趣的可以尝试一下。

参考：

什么是函数式编程思维？

编程范式游记（4）- 函数式编程

递归：如何用三行代码找到“最终推荐人”？

jerry.mei

基于 Redis 的分布式锁实践

微服务—如何注册和发现服务？

聊一聊 gRPC 的四种通信模式