leetcode：二叉树的坡度

描述：

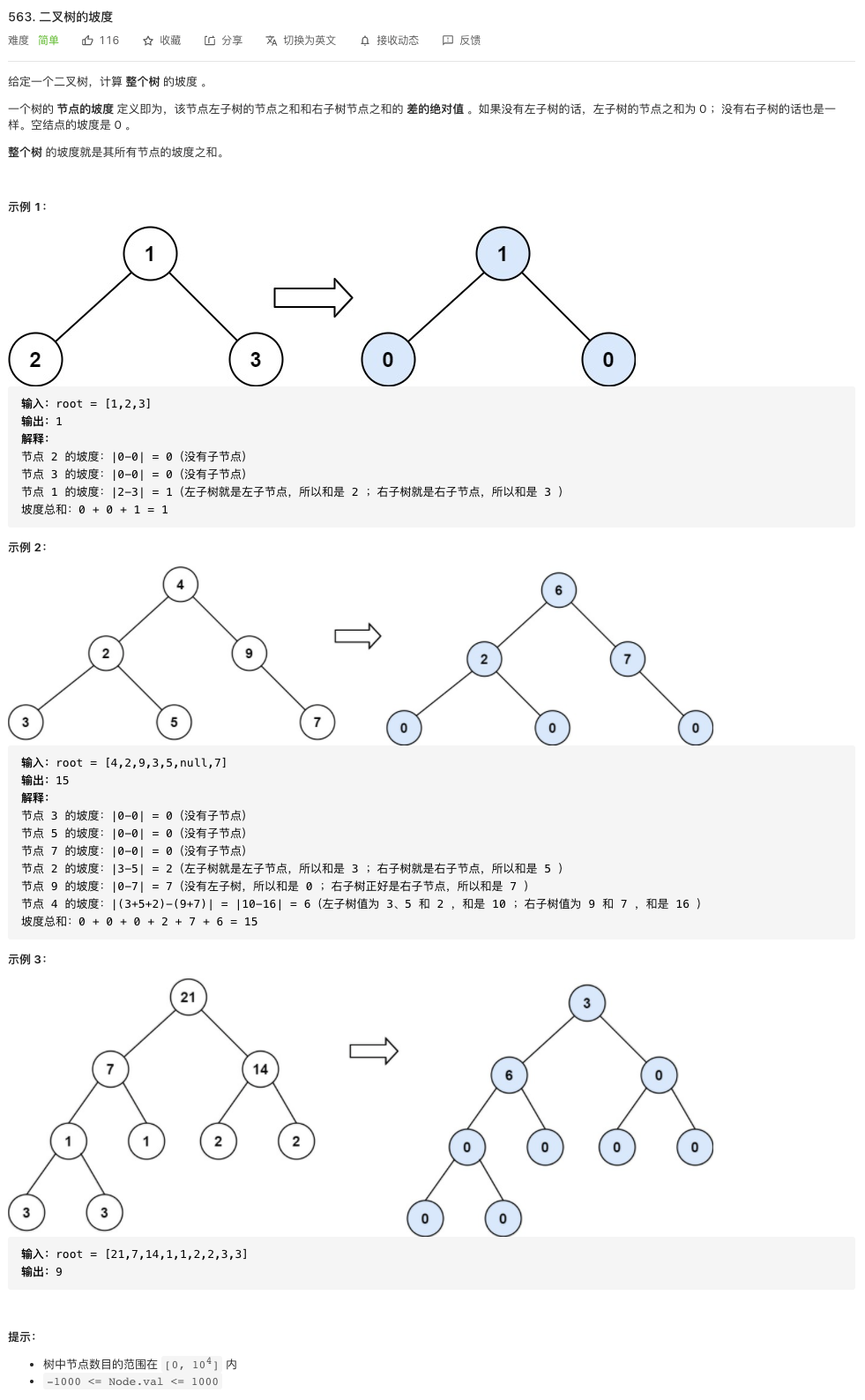
题解：

二叉树的问题用分治的思想来做都比较简单，这道题首先想到的就是递归。

我们要求21的坡度，其实就是求21的左子树上的结点之和以及右子树上的结点之和的差值。21的左子树上的结点之和 = 7 + 7的左子树之和 + 7的右子树之和，并且在求和的同时我们可以把坡度算出来。所以这道题其实就是递归地去求结点之和，求和的同时算出坡度。

那么我们利用递归算法的套路来解这道题：

第一步：明确递归函数干什么

在这里我们是计算结点之和，所以我们可以定义一个nodeSum的函数，它的目的就是求结点之和

function nodeSum(node) {}

第二步：找出基线条件

我们发现nodeSum(3) = 3 + nodeSum(3.left) + nodeSum(3.right)，但是3是没有子结点的，所以传进去的参数为空，所以基线条件就很好确定了。

if (node == null) {
    return 0;
}

第三步：找出递归条件

其实上面已经写出了递归条件

function nodeSum(node) {
    const leftSum = nodeSum(node.left);
    const rightSum = nodeSum(node.right);
    return leftSum + rightSum + node.val;
}

整个递归函数到这里就完成了，我们结合一下，最终的代码如下：

function nodeSum(node) {
  if (node == null) {
    return 0;
  }
  const leftSum = nodeSum(node.left);
  const rightSum = nodeSum(node.right);
  return leftSum + rightSum + node.val;
}

那么，这个跟我们这道题有什么关系呢？我们可以发现在求一个结点之和的时候，它的左结点之和和右结点之和我们都知道了，只要求一下它的差值就行了。3的坡度等于0，所以我们可以定义一个变量tilt来保存坡度，它的初始值为0，循环的时候累加就可以求出当前结点的坡度了。

最终算法如下：

ES6

export function findTilt(root) {
  let tilt = 0;
  nodeSum(root);

  function nodeSum(node) {
    if (node == null) {
      return 0;
    }
    const leftSum = nodeSum(node.left);
    const rightSum = nodeSum(node.right);
    tilt += Math.abs(leftSum - rightSum);
    return leftSum + rightSum + node.val;
  }

  return tilt;
}