线性表概念

线性表（List）：零个或多个数据元素的有限序列

抽象数据类型

ADT 线性表（List）

Data
    线性表的数据对象集合为{a₁, a₂..., a𝗇.}。数据元素之间的关系是一对一的关系
    
Operation
    InsertList(*L):         初始化操作，建立一个空的线性表L
    ListEmpty(L):           线性表为空，返回true；否则返回false
    ClearList(*L):          清空线性表
    GetElem(L, i, *e):      将线性表中第 i 个元素返回给 e
    LocateElem(L, e):       查找元素e，找到返回index，没找到返回-1
    ListInsert(*L, i, e):   在线性表的第 i 个位置插入元素 e
    ListDelete(*L, i, *e):  删除线性表的第 i 个位置元素，并用 e 返回其值
    ListLength(L):          返回线性表 L 的元素个数
    

线性表的顺序存储结构

线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素

1. 顺序存储结构的三个属性

• 存储空间的其实位置：数据data
• 线性表的最大存储容量：数组长度MaxSize
• 线性表的当前长度：length

注意：数组的长度是存放线性表的存储空间的长度，分配后一般是不可变的。线性表的长度是线性表中元素的个数。在任意时间，线性表的长度应该小于或等于数组的长度。

2. 数组的寻址计算公式

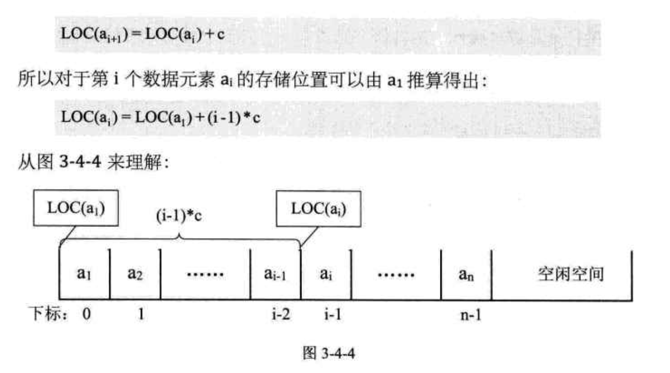
数组从零开始的公式为：LOC(aᵢ) = LOC(a₀) + i * c，每次CPU可以减少一次运算

3. 顺序存储结构的操作

获取元素

将线性表中的第 index 个位置的元素返回，也就是数组的index -1的下标，时间复杂度为：O(1)

/**
 * 线性表顺序存储结构获取 index 处的元素
 * @param {*} list
 * @param {*} index
 * @returns
 */
function getElem(list, index) {
  if (list.length == 0 || index < 1 || index > list.length) {
    return false
  }
  return list[index - 1]
}

插入元素

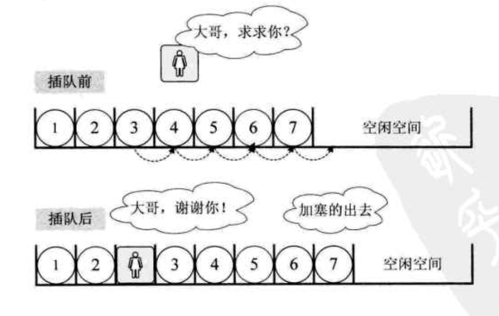
插入元素，需要将插入位置后面的元素全部向后挪一位，所以时间复杂度为O(n)。具体实现如下：

1. 如果插入位置不合理，抛出异常
2. 如果线性表的长度大于等于数组的长度，抛出异常或动态扩容
3. 从最后一个元素开始向前遍历到第 index 个位置，分别将它们都向后挪动一位
4. 将要插入的元素填入位置 index
5. 表长度加 1

/**
 * 线性表顺序存储结构的插入
 * @param {*} list 线性表
 * @param {*} index 插入的位置
 * @param {*} ele 插入的元素
 */
function listInsert(list, index, ele) {
  //如果插入的位置不对，返回错误
  //插入的位置可以是线性表中任意一个位置或者在线性表的末端插入，也就是list.length + 1
  if (index < 1 || index > list.length + 1) {
    return false
  }
  //若插入的位置不在表尾
  if (index <= list.length) {
    //将要插入位置后的数据元素向右移动一位
    let i = list.length - 1
    for (i; i >= index - 1; i--) {
      list[i + 1] = list[i]
    }
  }
  //插入新元素
  //list.length++;  js可以直接通过赋值的方式给数组扩容，不存在越界，所以不需要手动加长度
  list[index - 1] = ele
  return list
}

删除元素

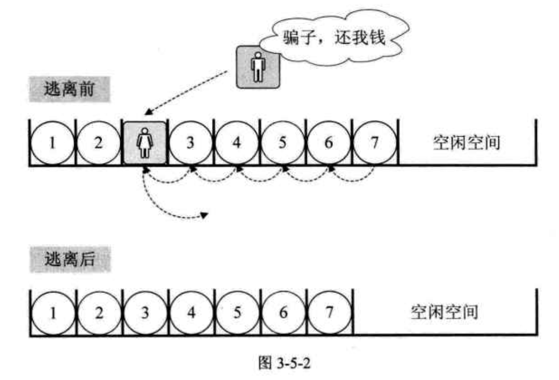
删除元素，跟插入元素类似，需要将删除位置后面的元素全部向前挪一位，所以时间复杂度为O(n)。具体实现如下：

1. 如果删除位置不合理，抛出异常
2. 取出删除元素
3. 从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前挪动一位
4. 表长度减 1

/**
 * 线性表顺序存储结构的删除
 * @param {*} list 线性表
 * @param {*} index 删除的位置
 */
function listDelete(list, index) {
  //线性表为空
  if (list.length == 0) {
    return false
  }
  //如果删除的位置不对，返回错误
  if (index < 1 || index > list.length) {
    return false
  }
  //取出删除位置的元素
  const ele = list[index - 1]
  //如果删除的不是最后位置
  if (index < list.length) {
    //将要删除的位置后的元素数据向左移动一位
    let i = index
    for (i; i < list.length; i++) {
      list[i - 1] = list[i]
    }
  }
  list.length--
  return ele
}

4. 线性表顺序存储结构的优缺点

优点：

• 无需为表示表中元素之间的逻辑关系而增加额外的存储空间
• 可以快速地存取表中任一位置的元素

缺点：

• 插入和删除操作需要移动大量元素

• 当线性表长度变化较大时，难以确定存储空间的容量

• 造成存储空间的”碎片“