leetcode：旋转图像

描述：

题解：

这道题要求使用原地算法，所以 rotate 方法不能有返回值。

思路一：使用辅助数组的方式，JS中需注意浅复制的问题。通过画图的方式可以得出核心逻辑：

const n = matrix.length
newMatrix[col][n - row - 1] = matrix[row][col]

实际上就是循环遍历这个二维数组，然后把结果填充到新的数组里面

ES6

function rotate(matrix) {
  // 这里复制的时候，注意不要用 slice 等浅拷贝的方法
  const newMatrix = matrix.map(arr => [...arr])

  // 规律：newMatrix[j][matrix.length - i - 1] = matrix[i][j]，通过画图就可以推理得到
  for (let i = 0; i < matrix.length; i++) {
    for (let j = 0; j < matrix[i].length; j++) {
      newMatrix[j][matrix.length - i - 1] = matrix[i][j]
    }
  }

  // 最后通过对 matrix 迭代修改值的方式保持引用
  for (let i = 0; i < matrix.length; i++) {
    for (let j = 0; j < matrix[i].length; j++) {
      matrix[i][j] = newMatrix[i][j]
    }
  }
}

时间和空间复杂度均为：O(n²)

思路二：使用原地旋转

这种思路刚好契合题目的考点，使用原地算法降低空间复杂度

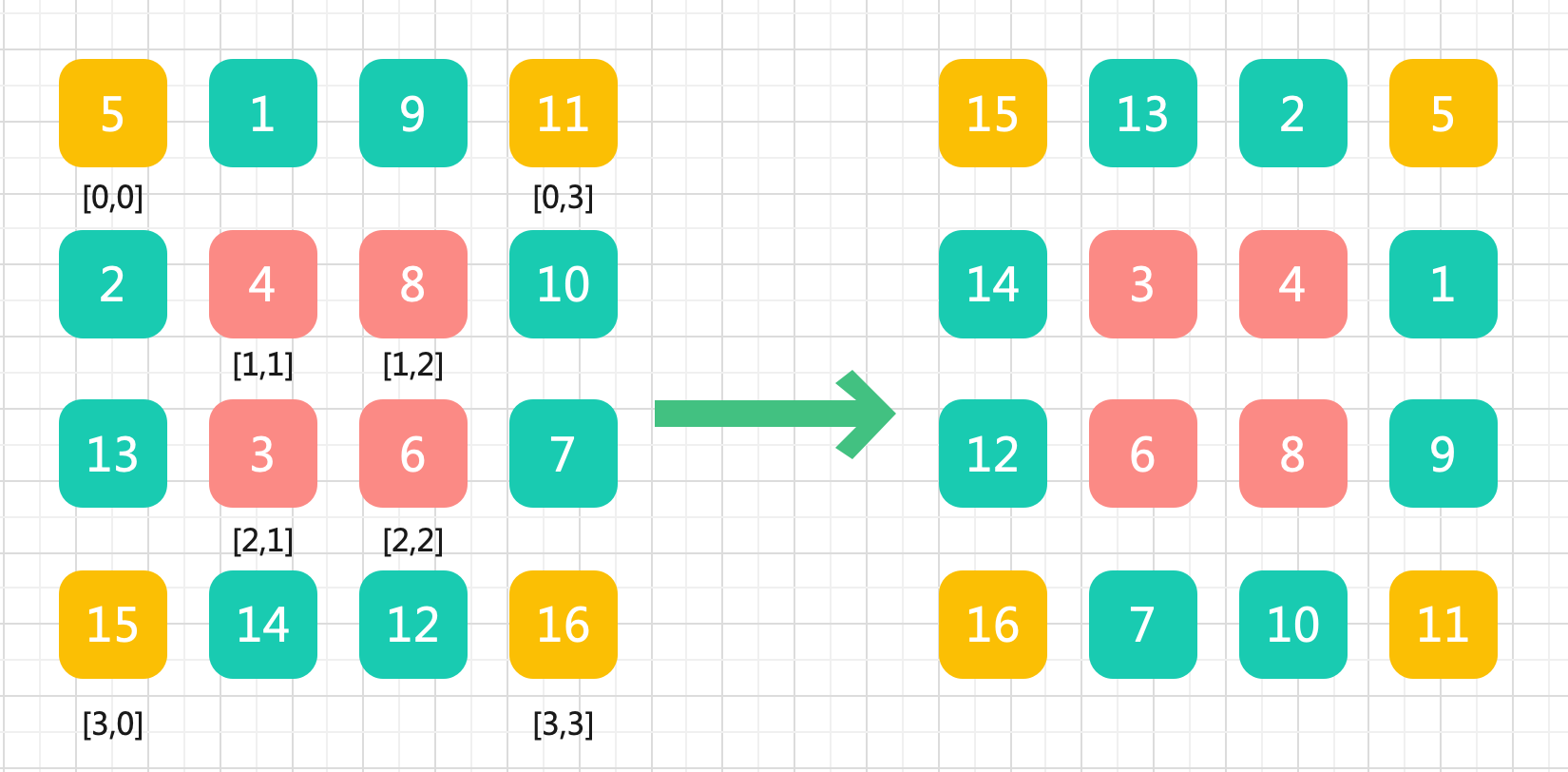
首先，我们使用题解一得出的核心逻辑然后转换一下思路：

matrix[row][col] = matrix[col][n - row -1]

比如：matrix[0][0]经过旋转变成 matrix[0][3]，我们可以得出一个关键等式：

matrix旋转之后的新位置

row = col
col = n - row -1

matrix之前的那个位置的值matrix[0][0]则是被matrix[3][0]替代，也就是原本的公式：

// matrix[0][0] = matrix[3,0]
matrix[col][n - row - 1] = matrix[row][col]

matrix之前的那个位置

col = row
n - row -1 = col //换算后就是
row = n - col -1

得到了上述的关系之后，我们用一个中间变量temp来保存第一个元素的位置，每次旋转涉及到4个数字的交换。

// 使用外圈来举例 matrix[0][0]
const temp = matrix[row][col]
// 旋转后，[0][0]处的值变成[3,0]处的值
matrix[row][col] = matrix[n - col -1][row]
// [3,0]处的值变成[3,3]处的值
matrix[n - col -1][row] = matrix[n - row -1][n - col - 1]
// [3,3]处的值变成[0,3]处的值
matrix[n - row -1][n - col - 1] = matrix[col][n - row -1]
// [0,3]处的值变成[0,0]处的值，也就是之前保存的 temp 变量
matrix[col][n - row -1] = temp

然后就是计算需要多少次交换轮回了。row方向我们可以发现从外圈到内圈，一共是n/2次；
col方向每次从row开始，为n - row - 1次。所以循环处理如下：

const n = matrix.length
  for (let row = 0; row < Math.floor(n / 2); row++) {
    for (let col = row; col < n - row - 1; col++) {
    }
  }

ES6

function rotate(matrix) {
  const n = matrix.length
  for (let row = 0; row < Math.floor(n / 2); row++) {
    for (let col = row; col < n - row - 1; col++) {
      const temp = matrix[row][col]
      matrix[row][col] = matrix[n - col - 1][row]
      matrix[n - col - 1][row] = matrix[n - row - 1][n - col - 1]
      matrix[n - row - 1][n - col - 1] = matrix[col][n - row - 1]
      matrix[col][n - row - 1] = temp
    }
  }
}

时间复杂度为O(n²)，空间复杂度为O(1)

思路三：使用翻转替代旋转

利用矩阵的特性，水平翻转然后沿主对角线翻转即可得到根旋转一样的结果

• 水平翻转

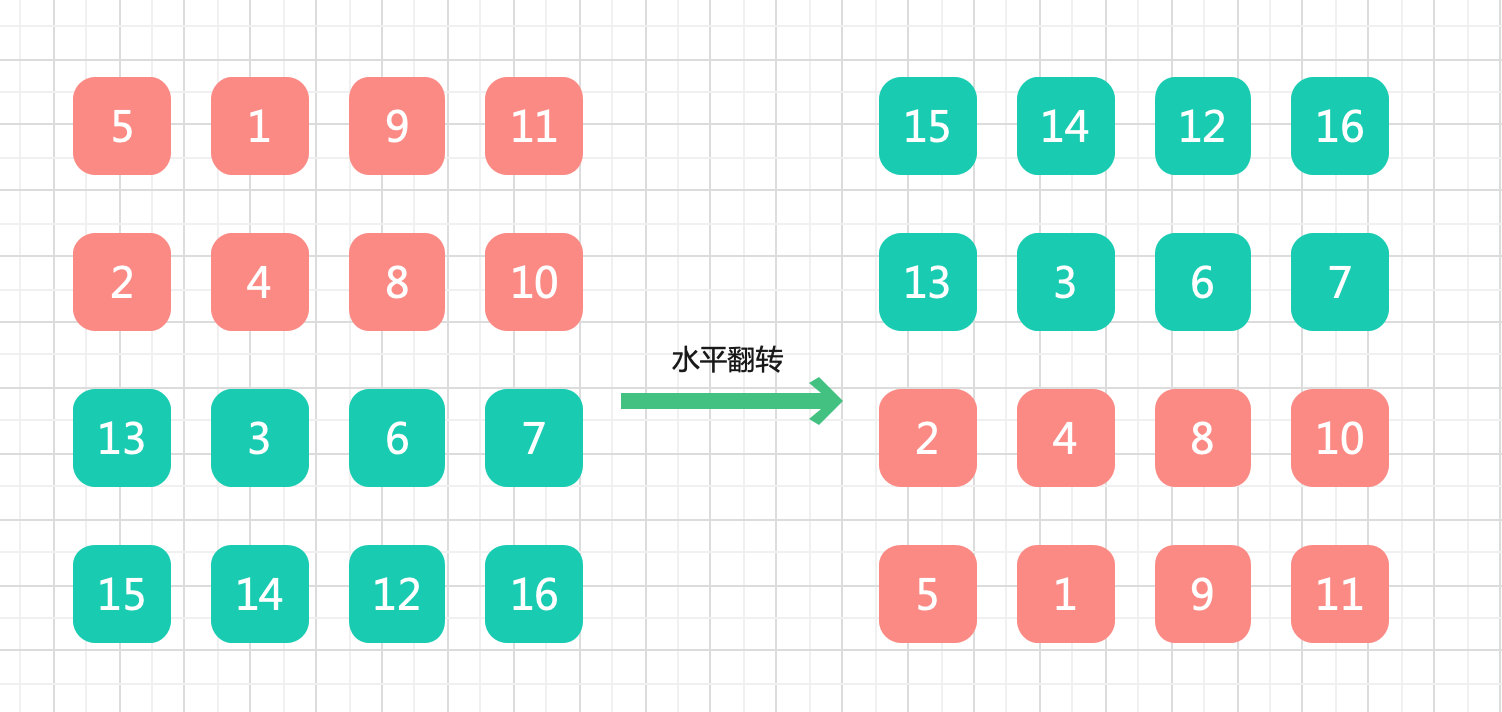
//水平翻转，row 进行交换，col 不变，交换次数是 n/2
matrix[row][col] = matrix[n−row−1][col]

• 沿主对角线翻转

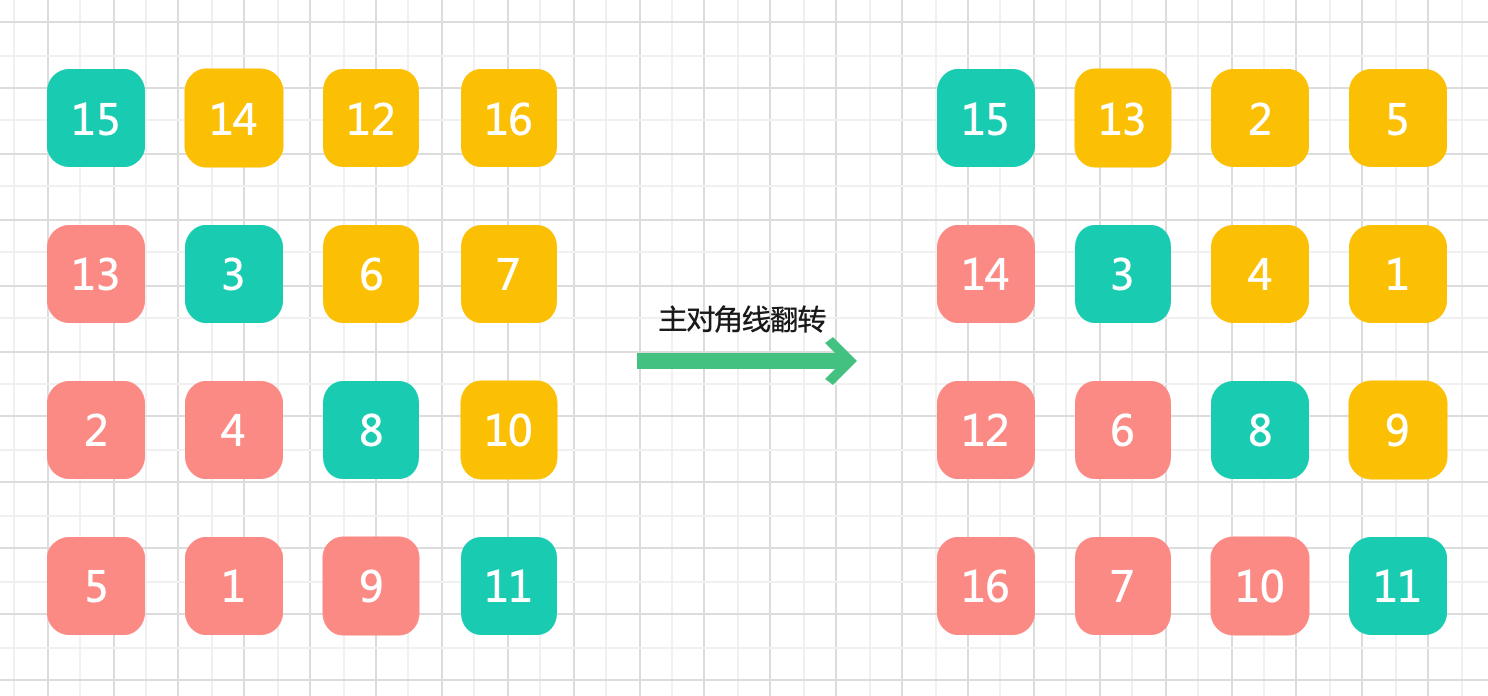
// 主对角线翻转，row 和 col 互相交换
matrix[row][col] = matrix[col][row]

// 交换次数，row 是从 0 到 n，col < row

ES6

function rotate(matrix) {
  const n = matrix.length
  //水平翻转
  for (let row = 0; row < Math.floor(n / 2); row++) {
    for (let col = 0; col < n; col++) {
      [matrix[row][col], matrix[n - row - 1][col]] = [matrix[n - row - 1][col], matrix[row][col]]
    }
  }
  //对角线翻转
  for (let row = 0; row < n; row++) {
    for (let col = 0; col < row; col++) {
      [matrix[row][col], matrix[col][row]] = [matrix[col][row], matrix[row][col]]
    }
  }
}

时间复杂度为：O(n²)，空间复杂度为O(1)