leetcode：对角线遍历

描述：

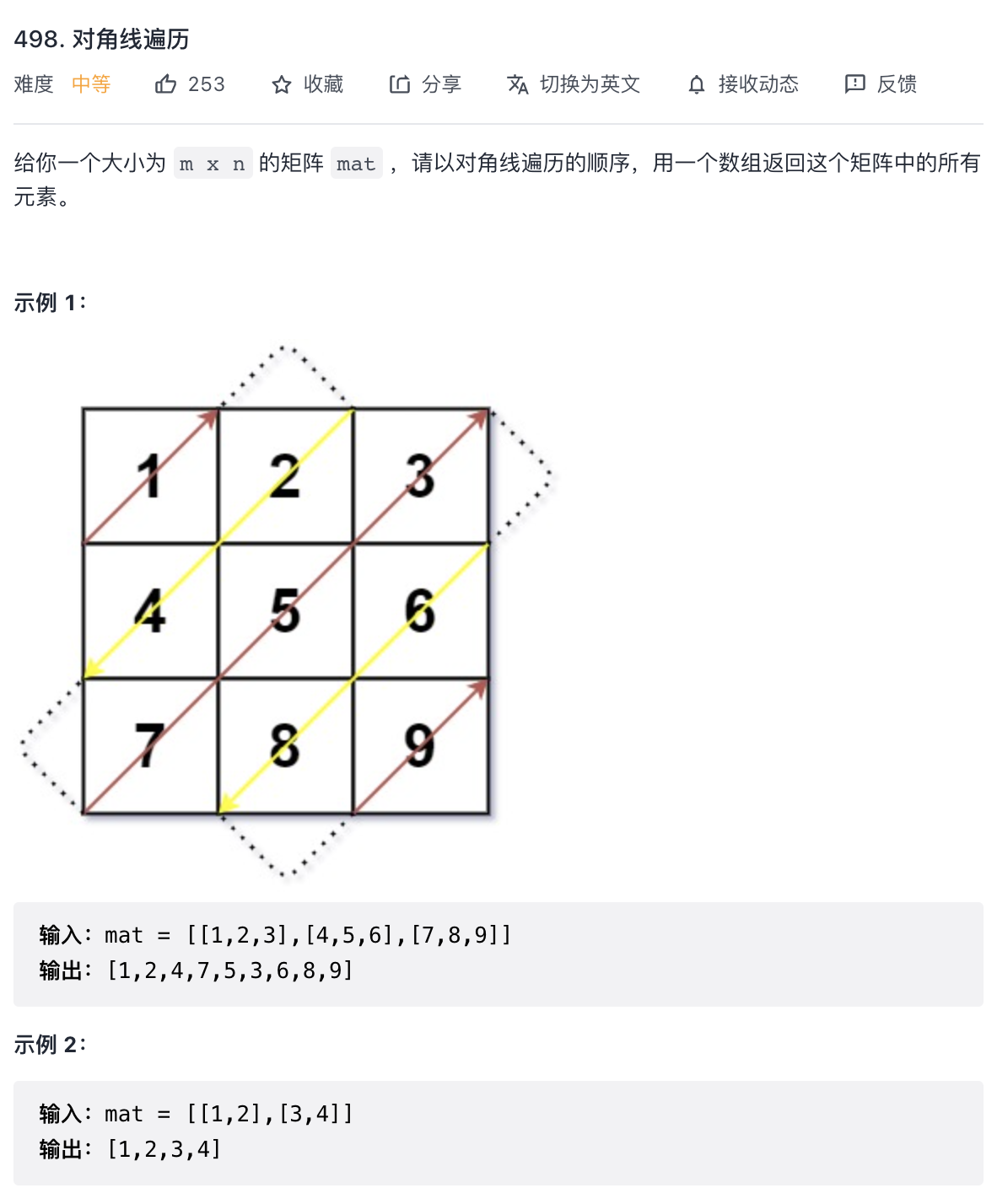
题解：

这道题可以完全通过找规律的方法解决。不过要注意分两种情况，即col为奇数或偶数。

首先，根据对角线的画法，我们可以发现对col进行遍历，然后输出每一个对角线的元素即可，先不考虑方向。下面是官方题解的示例图，我们可以参考一下：

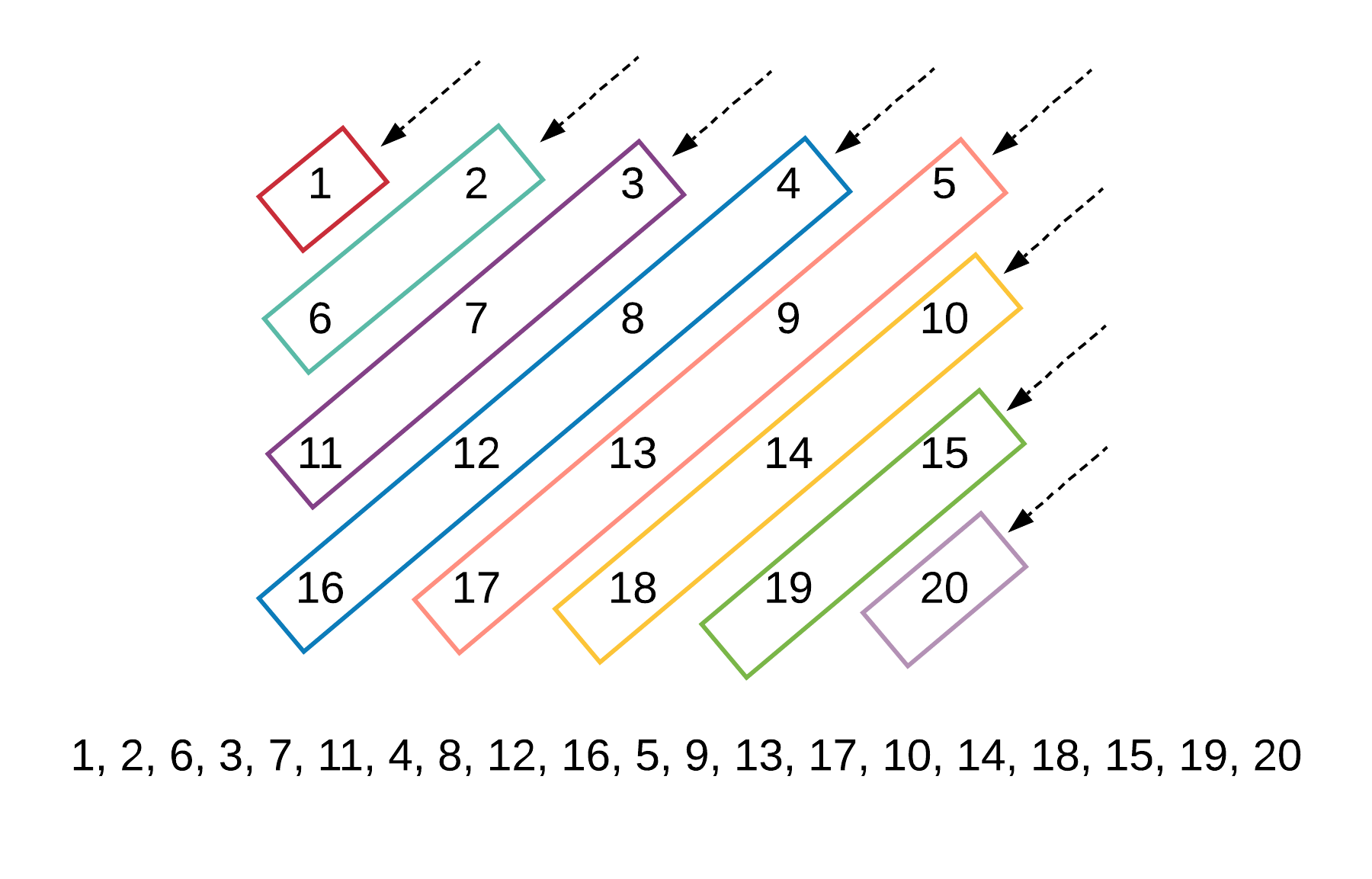
第一步：依次输出每个对角线的元素

每个对角线的元素输出，有一个很明显的规律。我们拿mat[0][2]即3这个元素举例。它的下一个元素满足以下规律：

mat[x][y] --->next == mat[x-1][y+1]

然后注意边界情况，即x>=0 && y<row。我们可以得出部分代码：

ES6

function findDiagonalOrder(mat) {
  // 矩阵的row和col，以及一个res数组
  const row = mat.length,
    col = mat[0].length,
    res = []

  for (let i = 0; i < col; i++) {
    //[xPos,yPos]起始值为每一个对角线的第一个元素
    let xPos = 0,
      yPos = i,
      arr = []
    while (yPos >= 0 && xPos < row) {
      arr.push(mat[xPos][yPos])
      xPos++
      yPos--
    }
    res.push(...arr)
  }
  return res
}

这时候输出了col个对角线的数据，即上图的5个对角线。然后剩下的[10, 14, 18, ...]我们也可以找出规律：

遍历row，然后内部算法跟上面的逻辑是一样的。因为第一行的[5, 9, 13, 17]我们已经处理了，所以循环是从1开始。我们补充完整的代码：

ES6

function findDiagonalOrder(mat) {
  // 矩阵的row和col，以及一个res数组
  const row = mat.length,
    col = mat[0].length,
    res = []

  for (let i = 0; i < col; i++) {
    //[xPos,yPos]起始值为每一个对角线的第一个元素
    let xPos = 0,
      yPos = i,
      arr = []
    while (yPos >= 0 && xPos < row) {
      arr.push(mat[xPos][yPos])
      xPos++
      yPos--
    }
    res.push(...arr)
  }

  for (let j = 1; j < row; j++) {
    let xPos = j,
      yPos = col - 1,
      arr = []
    while (yPos >= 0 && xPos < row) {
      arr.push(mat[xPos][yPos])
      xPos++
      yPos--
    }
    res.push(...arr)
  }
  return res
}

第二步：考虑需要反转的对角线

同样，我们分两部分分析。首先，我们发现上部分不论col为奇数或偶数都满足偶数列需要翻转数组。

下半部分就不太一样了。如果col为奇数，即上半部分最后一次箭头是朝上的，那么下半部分第一次就要朝下。即偶数行需要翻转。如果col为偶数，即奇数行需要翻转。

补充完整逻辑，如下：

ES6

export function findDiagonalOrder(mat) {
  // 矩阵的row和col，以及一个res数组
  const row = mat.length,
    col = mat[0].length,
    res = []

  for (let i = 0; i < col; i++) {
    //[xPos,yPos]起始值为每一个对角线的第一个元素
    let xPos = 0,
      yPos = i,
      arr = []
    while (yPos >= 0 && xPos < row) {
      arr.push(mat[xPos][yPos])
      xPos++
      yPos--
    }
    // 偶数列需要反转
    if (!(i & 1)) {
      arr.reverse()
    }
    res.push(...arr)
  }

  for (let j = 1; j < row; j++) {
    let xPos = j,
      yPos = col - 1,
      arr = []
    while (yPos >= 0 && xPos < row) {
      arr.push(mat[xPos][yPos])
      xPos++
      yPos--
    }
    //分两种情况，col为奇数时，j为偶数需要翻转；col为偶数时，j为奇数要翻转
    const needReverse = (col & 1 && !(j & 1)) || (!(col & 1) && j & 1)
    if (needReverse) {
      arr.reverse()
    }
    res.push(...arr)
  }
  return res
}