leetcode：二叉树的前序遍历

描述：

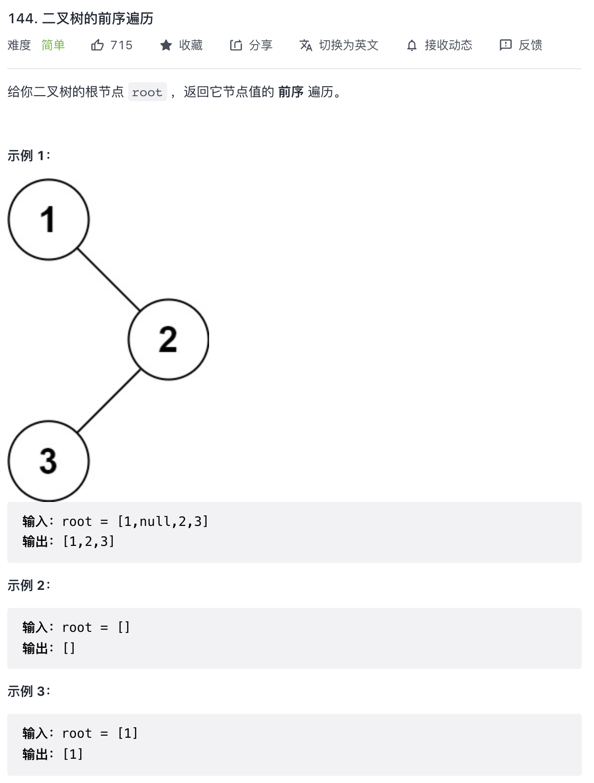
题解：

二叉树的前中后序遍历都可以用深度优先（DFS）算法来解决。深度优先的过程就是递归，递归本质上是一个栈。所以有两种方式，使用递归和栈。

前序遍历的过程如下：先访问根结点，然后前序遍历左子树，再前序遍历右子树

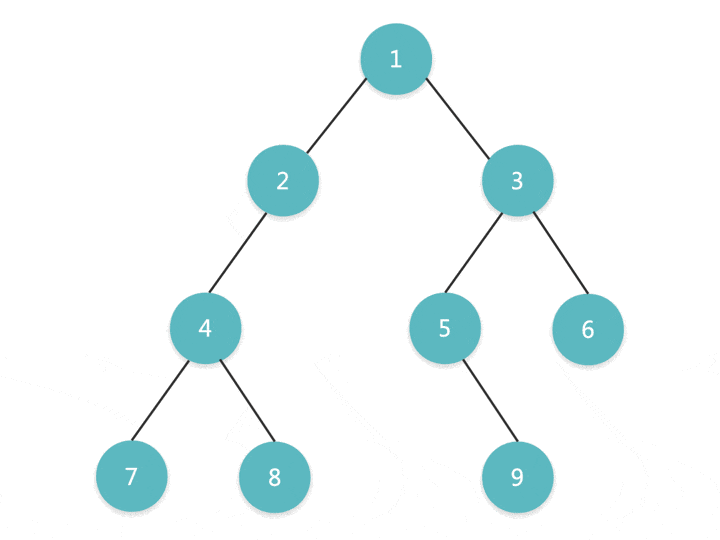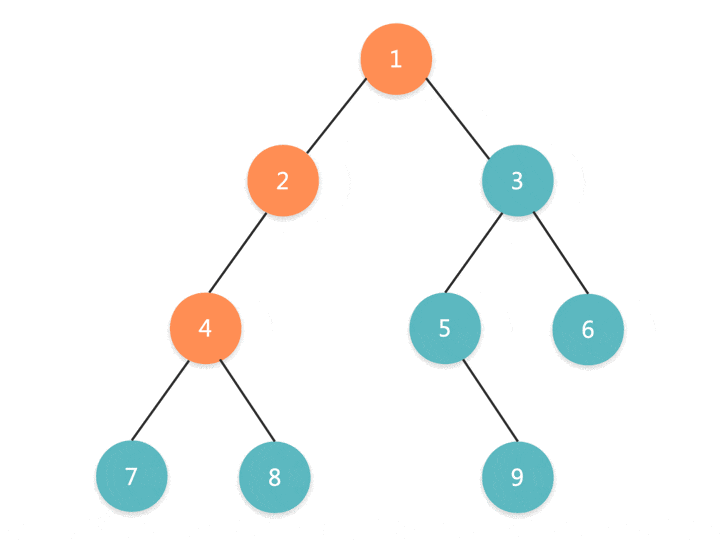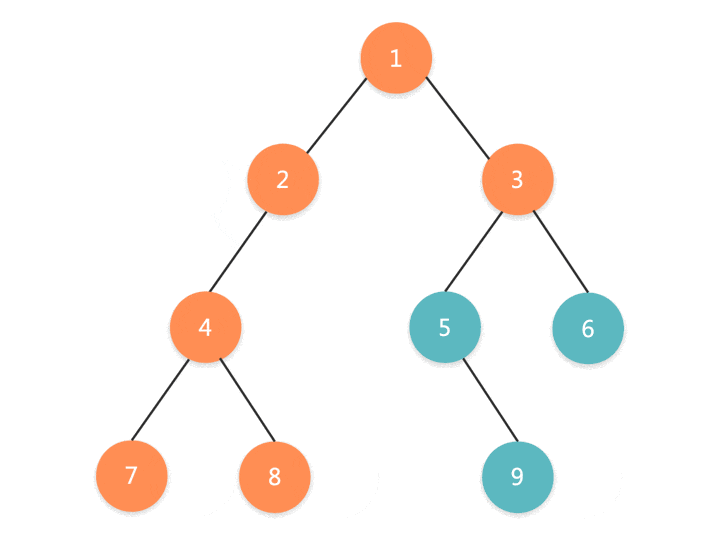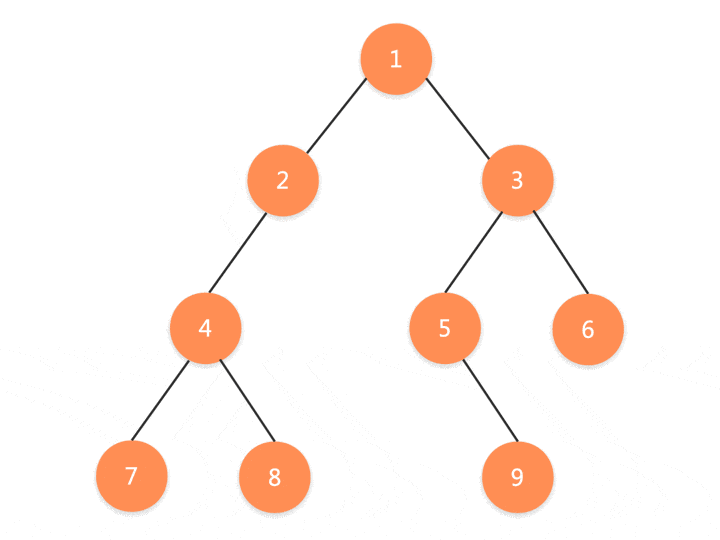
思路一：使用递归

递归记住三步走就行。

第一步定义一个递归的函数traversal

function traversal(root)

第二步找出基线条件，如果 root 不存在就结束了。

function traversal(root){
 if (root == null) {
      return
  }
}

第三步，使用分治的思想拆解问题，假设节点的子节点都遍历好了，我们只需要解决当前节点，也就是将它 push 到数组

最终实现如下：

function preorderTraversal(root) {
  const res = []
  traversal(root)
  return res
  function traversal(root) {
    if (root == null) {
      return
    }
    res.push(root.val)
    traversal(root.left)
    traversal(root.right)
  }
}

思路二：使用栈

递归的本质是栈，所以我们可以用一个栈来模拟这个过程。因为前序遍历是根节点 - 左子树 — 右子树这种方式遍历树。所以我们可以把根节点和它的左节点压入栈中，压栈的同时存入结果到数组中。如果没有左节点了，就出栈，然后处理它的右节点。

用语言描述不好理解，使用动图就可以很清晰地看出整个流程了：

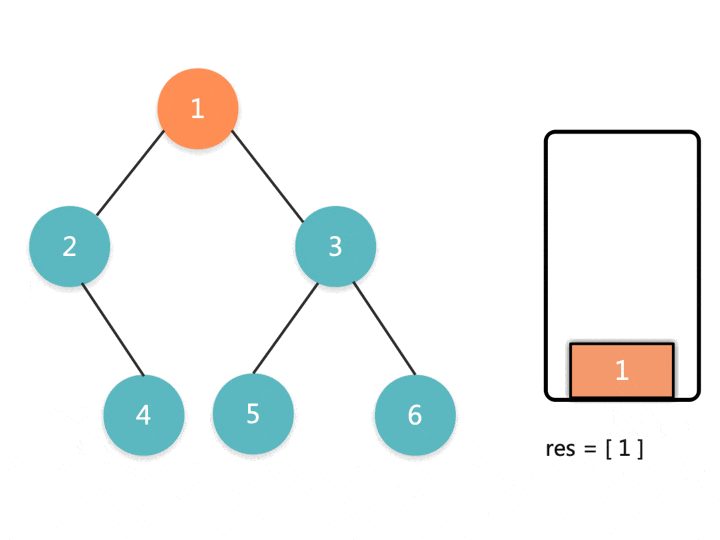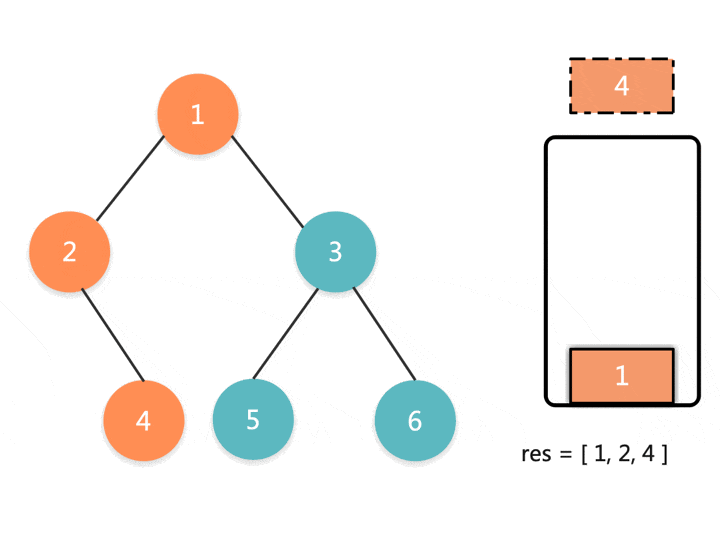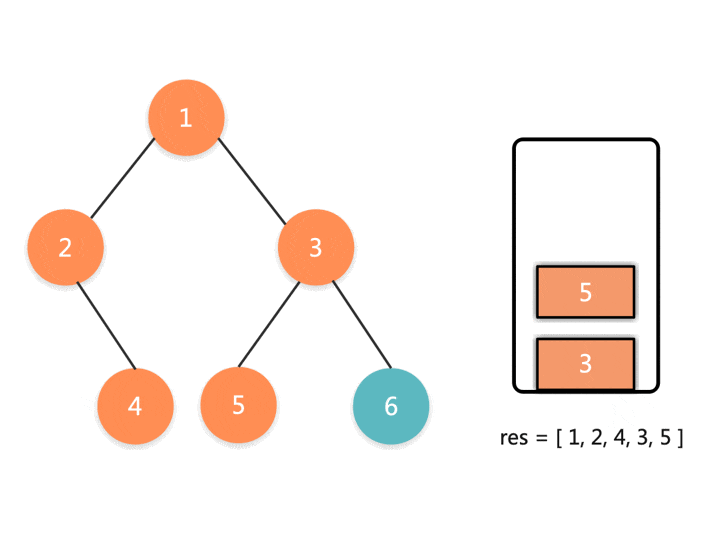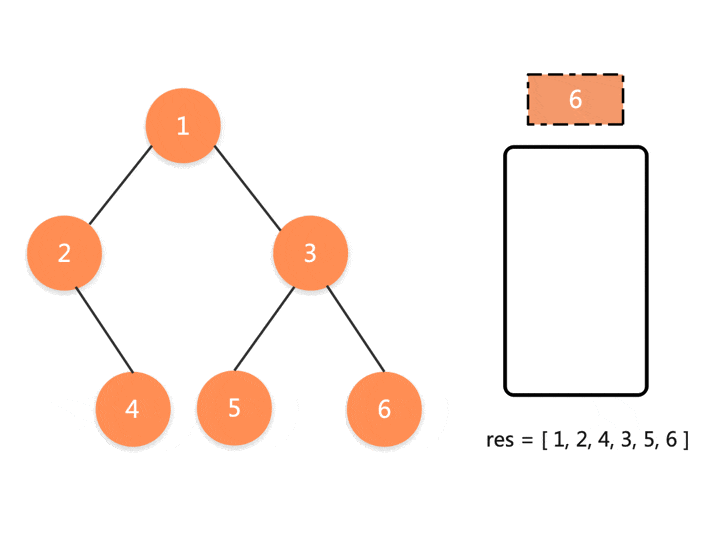
function preorderTraversal(root) {
  if (root == null) {
    return []
  }
  const res = []
  //模拟一个栈
  const stack = []
  stack.push(root)

  while (stack.length) {
    while (root) {
      //进栈的同时保存遍历的结果
      stack.push(root)
      res.push(root.val)
      root = root.left
    }
    //如果没有左节点了，出栈，处理右节点
    root = stack.pop()
    root = root.right
  }
  return res
}