leetcode：二叉树的层序遍历

描述：

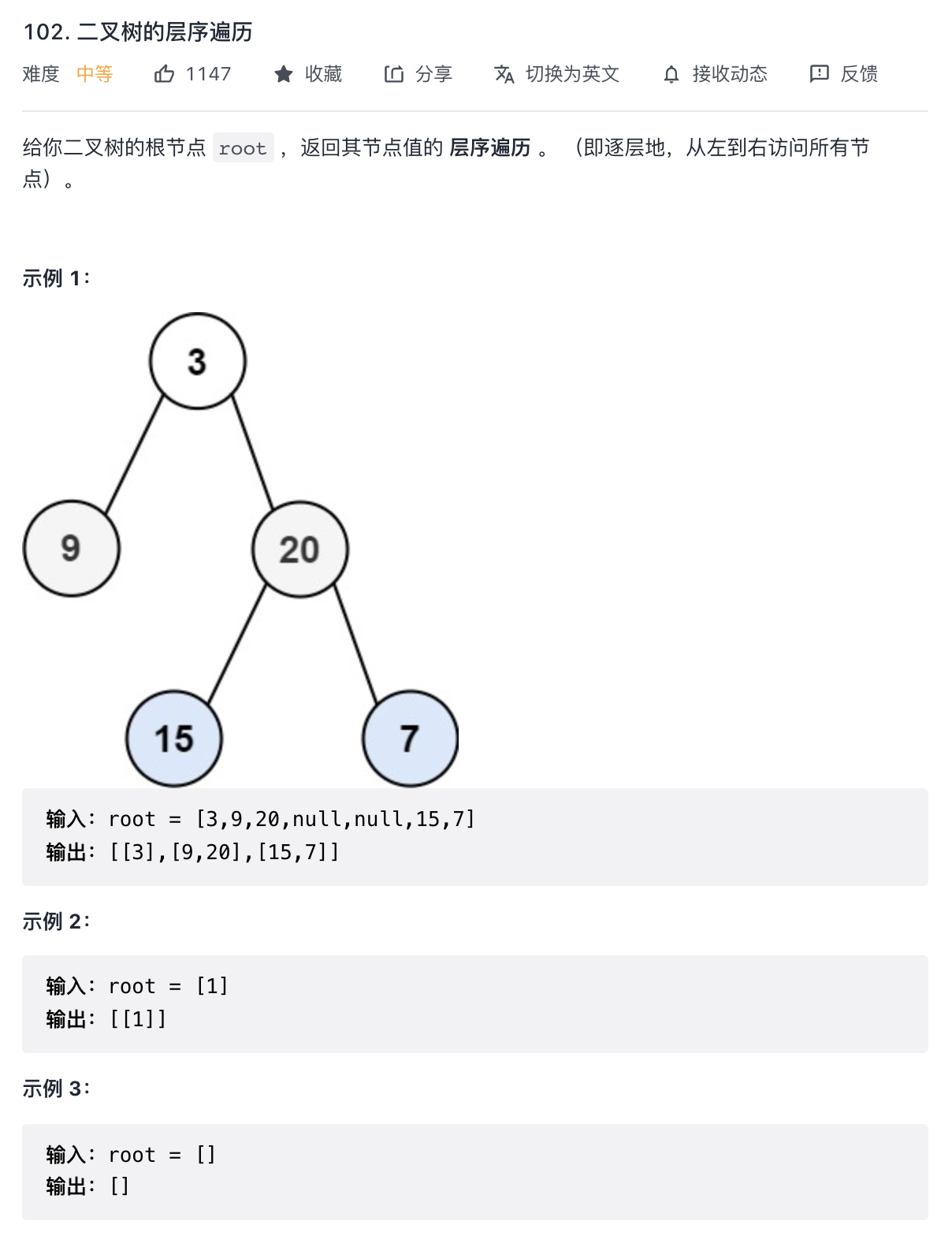
题解：

二叉树的遍历问题，记住几个要点就很好解决了：

• 树是特殊的图，所以树的遍历基本上都是用 BFS（广度优先搜索）和 DFS（深度优先搜索）来解决
• 对于树来说，前中后序遍历都可以用 DFS 来解决，使用递归或栈
• 树的层序遍历用 BFS 来解决，使用队列实现

思路一：使用递归

层序遍历也可以使用递归来实现，我们把它转换成森林的层序遍历，就可以保证递归的数据类型一致性问题。递归只要掌握了技巧，是十分简单的，可以参考这篇文章：掌握这些套路，轻松解决递归算法问题

我们分三步走，因为题目中的levelOrder的参数是root节点，我们要转换成森林，所以不能直接用该方法进行递归。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {};

第一步，明确函数干什么

定义一个traversal函数，它要做的事情就是层序遍历森林的节点，然后将结果保存在arr数组中

function traversal(nodes, arr) {}

第二步，找出基线条件

递归什么时候结束，我们发现如果传入的nodes为空，就直接结束

function traversal(nodes, arr) {
  if (nodes.length == 0) {
    return 
  }
}

第三步，使用分治的思想，将大问题拆小

我们拿例子中的9, 20这一层来举例，我们要层序遍历这一层，我们先假设它们的子节点的问题已经解决了，也就是如果有子节点，比如：20的子节点为15和7，我们对15 7使用traversal函数即可，伪代码如下：

traversal([15,7], arr)

然后我们来解决9, 20这一层的问题。我们发现只需要定义一个临时的数组，把 9 和 20 放进去，即tempArr = [9, 20]，然后将这个tempArr push 到 arr 中即可。

function traversal(nodes, arr) {
  //递归基线条件
  if (nodes.length == 0) {
    return
  }
  let tempNodes = [] //用来存放子节点
  let tempArr = [] //临时的数组， 用来存放每一层的遍历结果
  for (let node of nodes) {
    //将子节点push到tempNodes数组中，对他们进行递归调用
    if (!!node.left) {
      tempNodes.push(node.left)
    }
    if (!!node.right) {
      tempNodes.push(node.right)
    }
    tempArr.push(node.val)
  }
  //每一层的递归结果 push 到 arr 中
  arr.push(tempArr)
  traversal(tempNodes, arr)
}

然后我们处理一下边界情况，就可以了，完整代码实现如下：

ES6

function levelOrder(root) {
  //边界处理
  if (root == null) {
    return []
  }
  let arr = []
  //将根节点转换成森林，也就是[root]，对它进行递归
  traversal([root], arr)
  return arr

  function traversal(nodes, arr) {
    //递归基线条件
    if (nodes.length == 0) {
      return
    }
    let tempNodes = [] //用来存放子节点
    let tempArr = [] //临时的数组， 用来存放每一层的遍历结果
    for (let node of nodes) {
      //将子节点push到tempNodes数组中，对他们进行递归调用
      if (!!node.left) {
        tempNodes.push(node.left)
      }
      if (!!node.right) {
        tempNodes.push(node.right)
      }
      tempArr.push(node.val)
    }
    //每一层的递归结果 push 到 arr 中
    arr.push(tempArr)
    traversal(tempNodes, arr)
  }
}

思路二：使用 BFS，借助队列实现

这道题跟传统的 BFS 不一样，我们可以看一下演示过程。传统的 BFS 我们遍历出来的是一个一维数组，无法区分是哪一层。

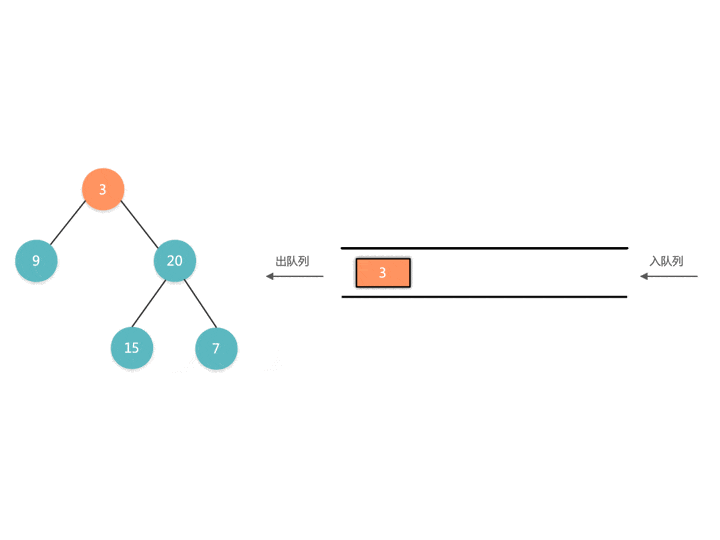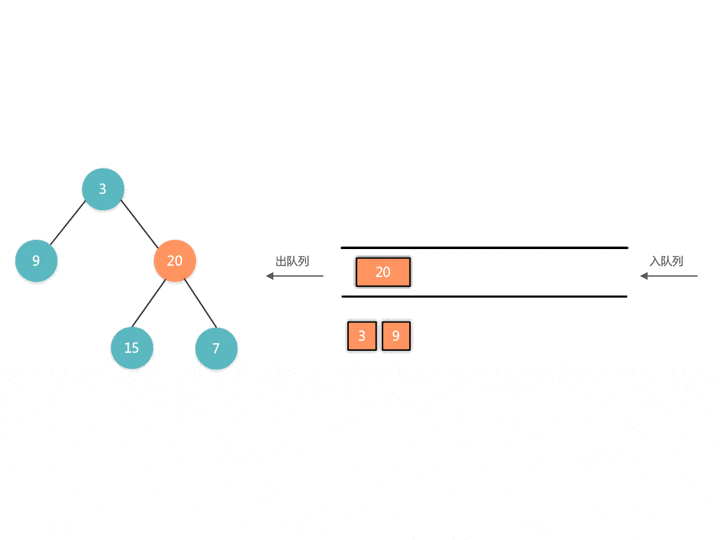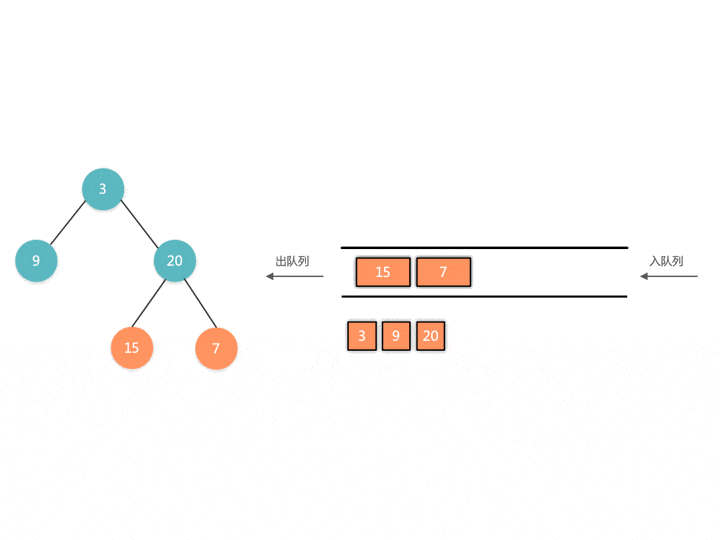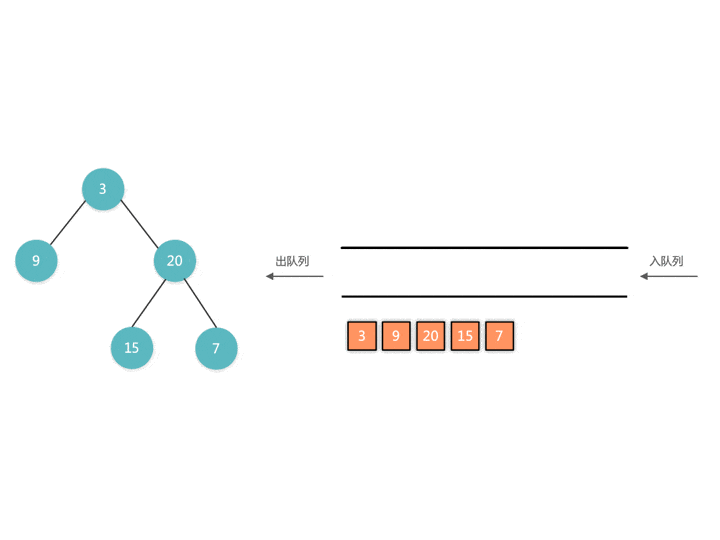
传统BFS实现

function levelOrder(root) {
  const res = [];
  const queue = []; //使用数组模拟一个队列
  queue.push(root);
  while (queue.length) {
    root = queue.shift();
    res.push(root.val);
    if (!!root.left) {
      queue.push(root.left);
    }
    if (!!root.right) {
      queue.push(root.right);
    }
  }
  return res;
}

题目的结果是要得到一个二维数组，可以区分是哪一层的节点，我们需要做一下变形。

在每一层遍历的开始时，我们先记录一下队列中节点的数量 n（也就是这一层的节点个数），然后一口气处理完这一层的节点。

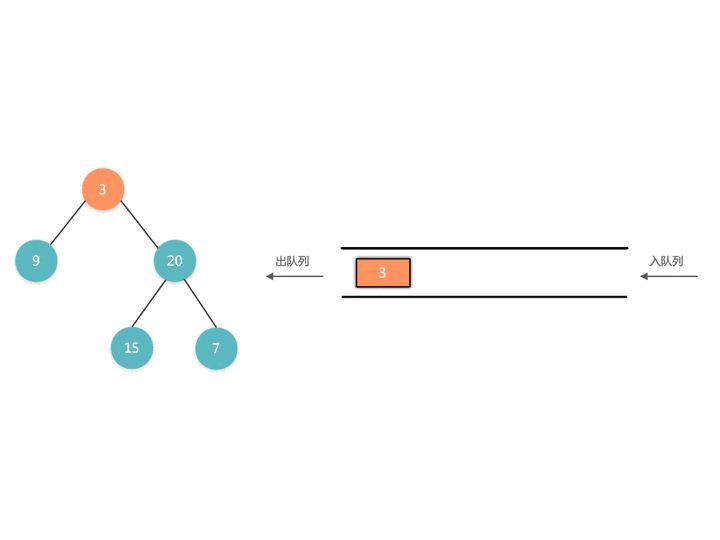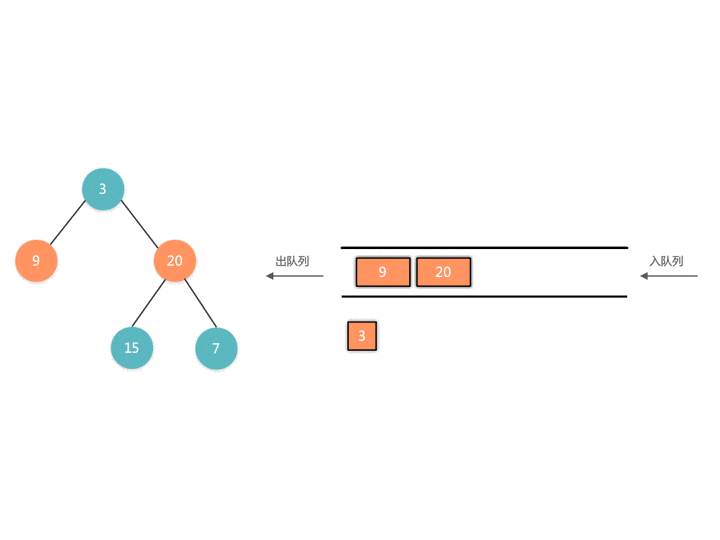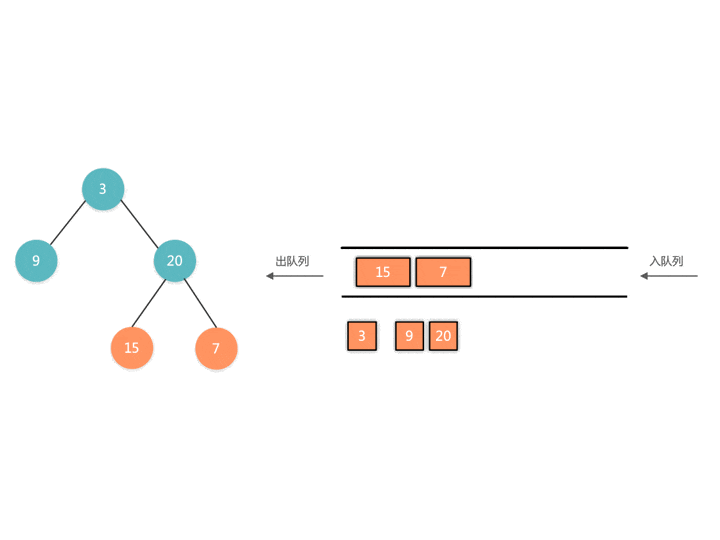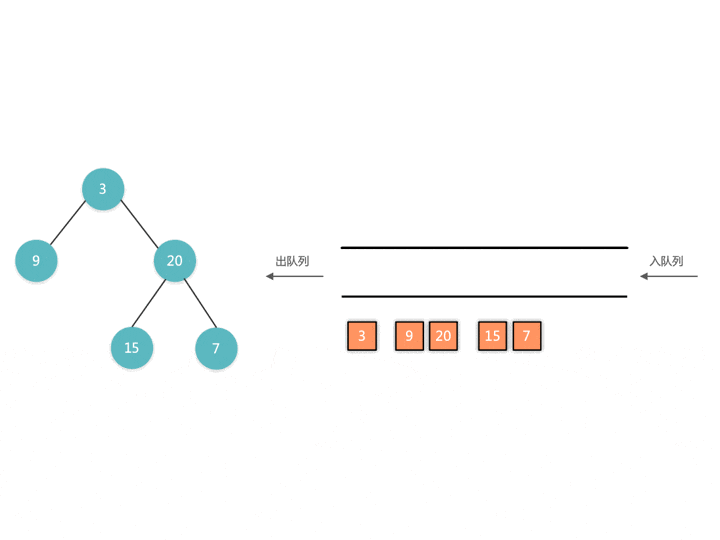
代码实现如下：

function levelOrder(root) {
  //异常处理
  if (root == null) {
    return []
  }
  const res = [] //最终的结果
  const queue = [] //用数组模拟队列
  queue.push(root)

  while (queue.length) {
    //用一个临时数组保存每一层遍历的结果
    const tempArr = []
    //每一层遍历前，记录一下该层的节点个数
    const queueSize = queue.length
    for (let i = 0; i < queueSize; i++) {
      //内部逻辑跟传统BFS一样
      root = queue.shift()
      tempArr.push(root.val)
      if (!!root.left) {
        queue.push(root.left)
      }
      if (!!root.right) {
        queue.push(root.right)
      }
    }
    //把每一层遍历的结果push到res中
    res.push(tempArr)
  }
  return res
}

思路二改进：不使用临时数组

不用临时数组的话，我们可以在每一层开始遍历前，像 res 中 push 一个空数组，然后将结果依次 push 到该空数组中即可。

function levelOrder(root) {
  //异常处理
  if (root == null) {
    return []
  }
  const res = [] //最终的结果
  const queue = [] //用数组模拟队列
  queue.push(root)

  while (queue.length) {
    //每一层开始遍历前，先push一个空数组到res中
    res.push([])
    //每一层遍历前，记录一下该层的节点个数
    const queueSize = queue.length
    for (let i = 0; i < queueSize; i++) {
      //内部逻辑跟传统BFS一样
      root = queue.shift()
      //找到末端的空数组，push到该数组
      res[res.length - 1].push(root.val)

      if (!!root.left) {
        queue.push(root.left)
      }
      if (!!root.right) {
        queue.push(root.right)
      }
    }
  }
  return res
}