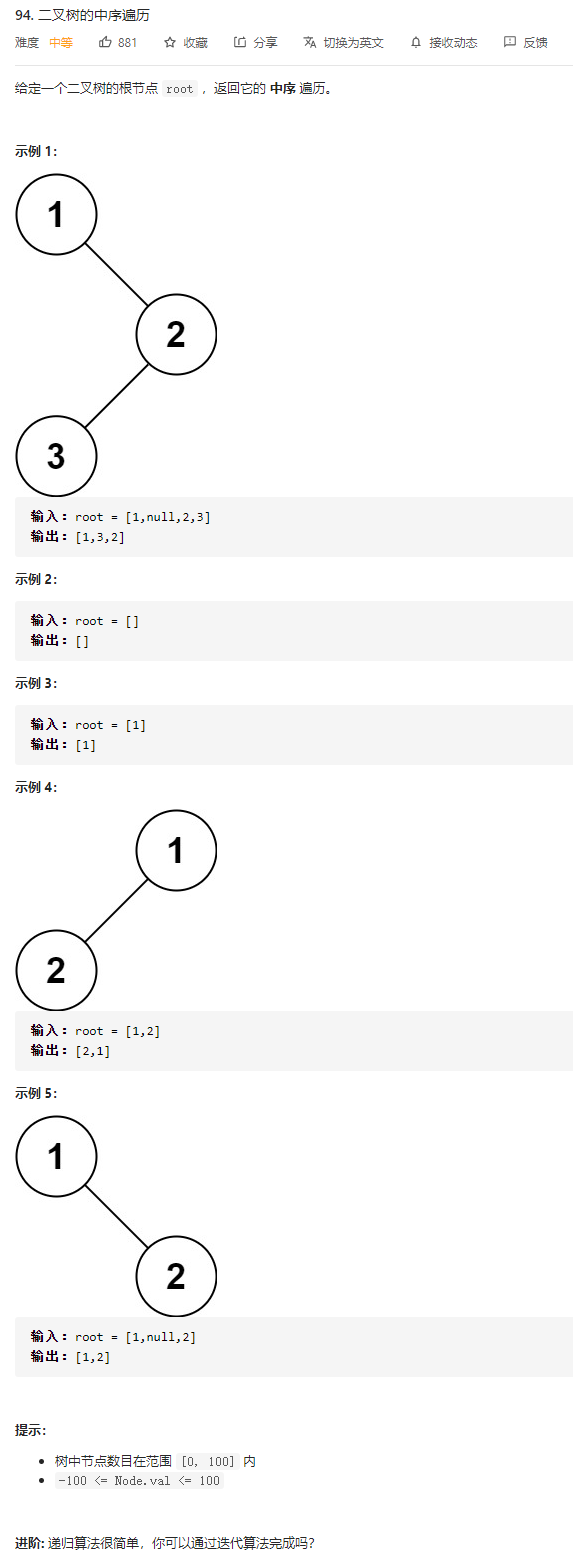
leetcode：二叉树的中序遍历

描述：

题解：

思路一：递归

二叉树的中序遍历就是按照访问左子树 — 根节点 — 右子树 的方式遍历这棵树。对于这种问题想都不用想，递归最简单了。

ES6

export function inorderTraversal(root) {
  function traversal(root) {
    if (!!root.left) {
      traversal(root.left);
    }
    arr.push(root.val);
    if (!!root.right) {
      traversal(root.right);
    }
  }
  let arr = [];
  if (root == null) {
    return [];
  }
  traversal(root);
  return arr;
}

思路二：借助栈

题目的进阶要求是使用迭代算法来完成。我们知道，递归本质上是调用栈。使用迭代算法的话，我们显式地去维护一个栈就可以了。

我们可以画图分析一下。假设我们的二叉树是[1,2,3,4,5,6,null,null,null,7]，一开始我们初始化一个空的栈。

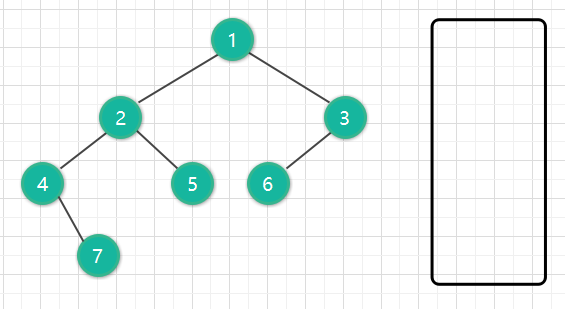
然后，因为我们是按照访问左子树 — 根节点 — 右子树 的方式遍历这棵树。所以根节点以及它的所有子节点先进栈。

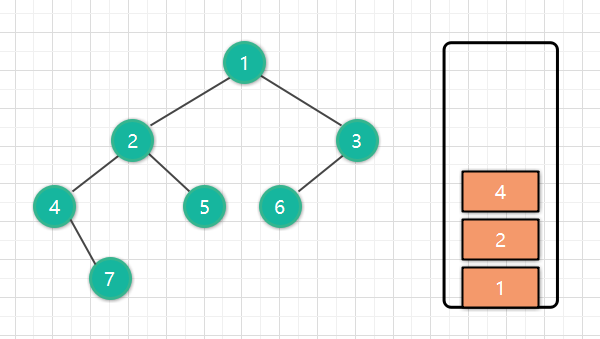
这时候 4没有左节点了，所以4出栈，我们把访问过的4保存到数组中，res = [4]。

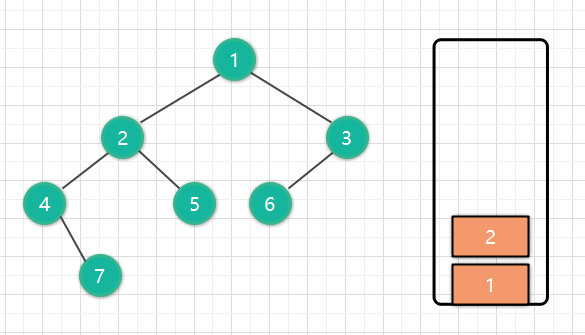
然后对右节点7做同样的操作。也就是7以及它的所有左节点进栈。

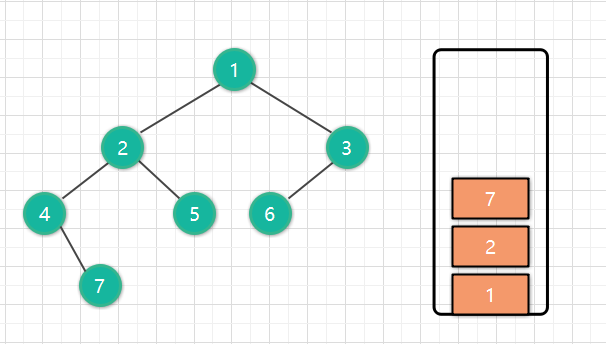
7没有左节点了，所以7出栈，我们把访问过的7也保存到数组中，res = [4,7]。此时，7没有右节点了，我们看到栈顶现在是2，我们开始处理2这个结点。

对于2，我们直接访问2，然后再操作2的右节点即可，也就是2出栈，5进栈。res = [4,7,2]

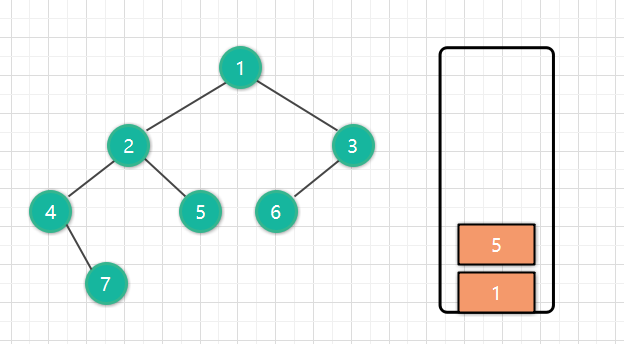
接下来都是重复这样的动作。通过图解的方式，我们的代码基本上已经浮现出来了。

ES6

export function inorderTraversal1(root) {
  const res = [];
  const stack = [];
  while (root || stack.length) {
    while (root) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    res.push(root.val);
    root = root.right;
  }
  return res;
}