leetcode：平衡二叉树

描述：

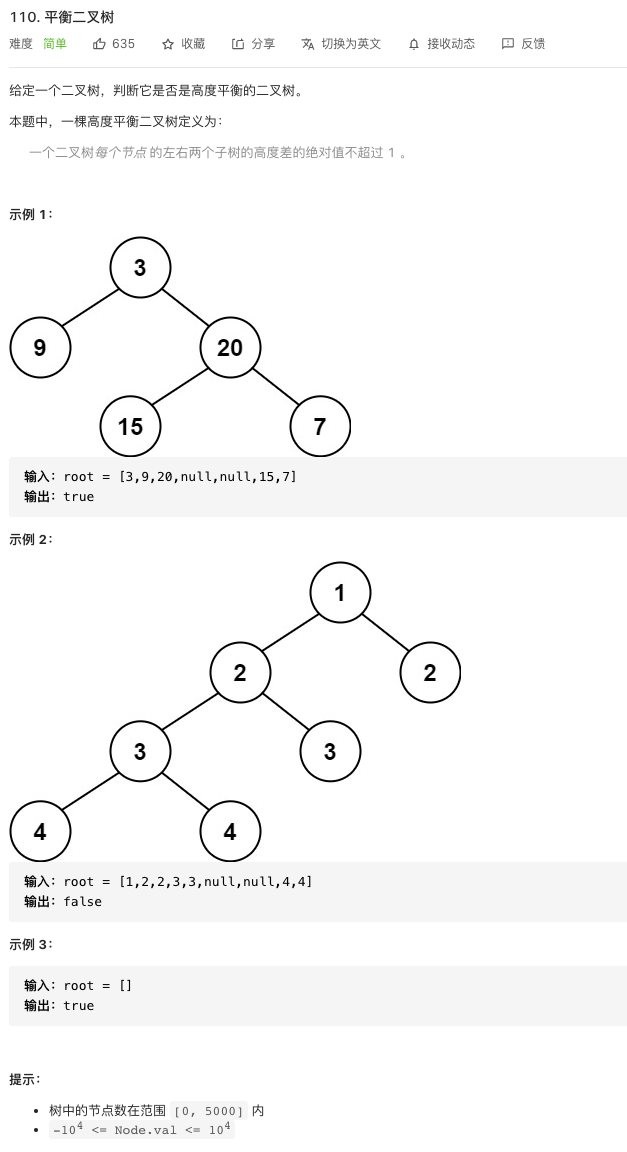
题解：

根据平衡二叉树的定义，我们可以知道这道题本质上就是递归地求二叉树每个结点的高度。递归的顺序我们可以采用自顶向下或自底向上的顺序。求二叉树的高度我们可以采用层序遍历来做。

思路一：自顶向下递归

自顶向下的递归类似二叉树的前序遍历。先检查当前结点的左右子树的高度是否相差超过1。如果不超过1，再分别递归检查它的左子树和右子树。

ES6

export function isBalanced(root) {
  if (root == null) {
    return true;
  } else {
    let leftDeep = 0,
      rightDeep = 0;
    if (root.left) {
      leftDeep = levelOrderTraverse([root.left], 0);
    }
    if (root.right) {
      rightDeep = levelOrderTraverse([root.right], 0);
    }
    //二叉树每个结点的左右两个子树的高度差的绝对值不超过1
    return (
      Math.abs(leftDeep - rightDeep) <= 1 &&
      isBalanced(root.left) &&
      isBalanced(root.right)
    );
  }

  /**
   * 层序遍历求二叉树的高度
   * @param {*} nodes
   * @param {*} deep
   * @returns
   */
  function levelOrderTraverse(nodes, deep) {
    if (nodes.length == 0) {
      return deep;
    }
    deep++;
    let temp = [];
    for (let item of nodes) {
      if (item.left != null) {
        temp.push(item.left);
      }
      if (item.right != null) {
        temp.push(item.right);
      }
    }
    return levelOrderTraverse(temp, deep);
  }
}

时间复杂度：O(n²)

思路二：自顶向下递归，优化二叉树的高度算法

求二叉树的高度前面写得有点复杂，其实有更简单的办法。我们只需要取它的左右结点高度的最大值+1即可。公式：

height(p)= 0 when p == null
height(p) = max(height(p.left),height(p.right))+1 when p != null

ES6

export function isBalanced(root) {
  if (root == null) {
    return true;
  }
  return (
    Math.abs(height(root.left) - height(root.right)) <= 1 &&
    isBalanced(root.left) &&
    isBalanced(root.right)
  );

  /**
   * 求二叉树的高度
   * @param {*} nodes
   * @returns
   */
  function height(root) {
    if (root == null) {
      return 0;
    }
    return Math.max(height(root.left), height(root.right)) + 1;
  }
}

时间复杂度：O(n²)

思路三：自底向上的递归

上面的思路由于前序遍历要对每一个结点遍历去求高度，所以时间复杂度为O(n²),比较高。我们可以换个思路，使用自底向上的递归方式。自底向上的方式类似二叉树的后续遍历，对于当前遍历到的结点，我们先递归地判断它的左右子树是否平衡，再判断以当前节点为根节的子树是否平衡。如果是平衡的，我们返回树的高度，否则返回-1。所以我们最终判断树的高度大于等于0即可。

ES6

export function isBalanced(root) {
  return height(root) >= 0;
  /**
   * 自底向上求高度，-1代表已经不平衡了。只要任意结点不平衡，就不是平衡二叉树了。
   * @param {*} nodes
   * @returns
   */
  function height(root) {
    if (root == null) {
      return 0;
    }
    const leftHeight = height(root.left);
    if (leftHeight == -1) {
      return -1;
    }
    const rightHeight = height(root.right);
    if (rightHeight == -1) {
      return -1;
    }
    if (Math.abs(leftHeight - rightHeight) > 1) {
      return -1;
    }
    return Math.max(leftHeight, rightHeight) + 1;
  }
}

时间复杂度：O(n)